Pressure Project 3: Trailblazing
Posted: December 4, 2017 Filed under: Calder White, Paper & Pen, Pen and Pencil Games, Pressure Project 3, Uncategorized Leave a comment »For our third Pressure Project, our prompt was to take a pen & paper game and combine it with another game to make a delightfully replayable hybrid that had no more than 5 rules and did not require the creator’s verbal or gestural intervention. I love to play card games, and especially drinking games involved with cards, and so I decided to figure out a way in which I could revamp one of my favourite drinking card games — Ride the Bus — to suit this assignment.
For those who don’t know, Ride the Bus is a drinking game played with two people. The dealer lays out five cards and flips the first one. The second player then goes through a sequence of questions guessing the nature of the proceeding cards in this order:
- Is the second card higher or lower than the first card?
- Is the third card inside of (between) or outside of the first two cards?
- Is the fourth card red or black?
- What is the suit of the last card?
The catch is this: if at any point the second guesser makes an incorrect guess, they have to take a drink, a new set of five cards is dealt, and the game restarts. The player only wins once they “ride the bus” to the end.
Taking some inspiration from tic-tac-toe and Connect 4, I was curious about how Ride the Bus could function if placed in a grid. I decided that the cards would be set up in a 5×5 grid and this would become a game about which player — the dealer or the guesser — could collect the most cards by the end. Instead of having to drink for guessing a card incorrectly, an incorrect guess simply signaled the end of a player’s turn and therefore a stunted chance at collecting more cards.
The instruction sheet of my hybrid game can be found here: ACCADTrailblazing
In the end, this game reminded me a lot of afternoon’s spent at my Baba’s house playing War for hours. Although perhaps not the most stimulating for adults, Trailblazing could easily be an entertaining children’s or family game, and definitely gets more fun the more you play it!
folding_fours game
Posted: December 16, 2016 Filed under: Paper & Pen Leave a comment »Playing connect four as part of class was a great experience!
Encouraged by Alex to find new possibilities, me and Ece figured a new challenge in this old game by adding the possibility of folding the paper every third turn. This, after going deeper on the game with Ashlee, added a new experience: materiality.
The folding of the paper makes a richer physical level experience.
Disruption
Posted: September 6, 2015 Filed under: Anna Brown Massey, Paper & Pen Leave a comment »Instruction: play a “paper & pen” game, and change one rule
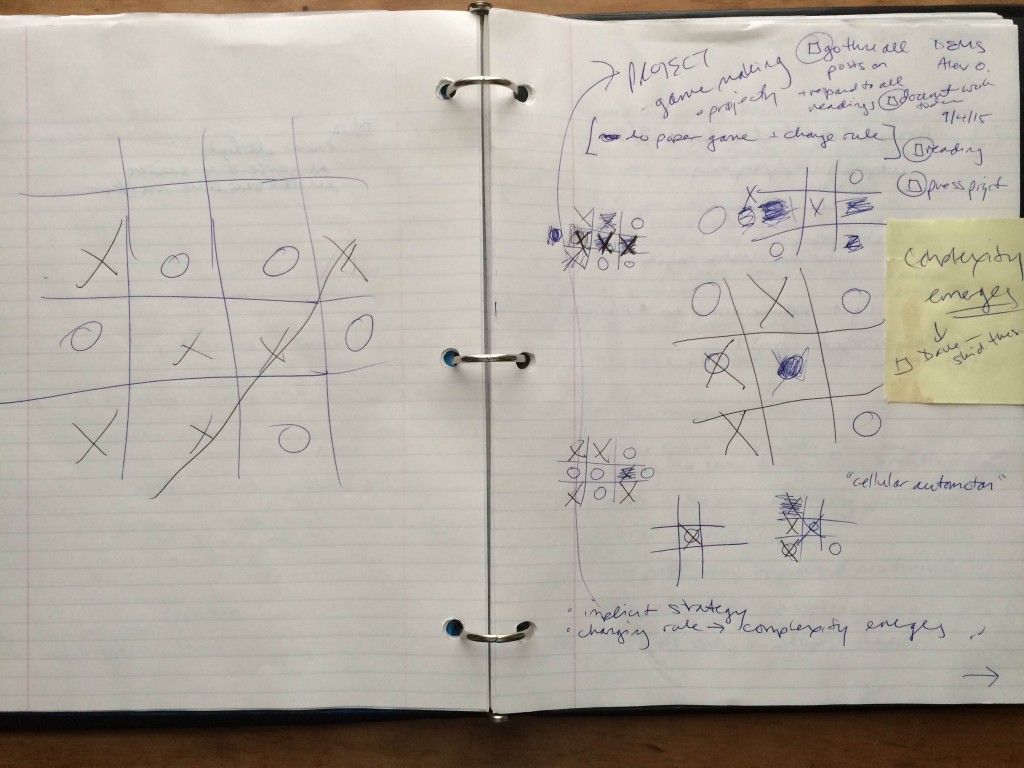
Partner Jonathan and I chose tic-tac-toe.
Reading from left to write, we played “normally”, with J. initiating with an “x” in the center square. The game was a draw, so we experimented with our first rule:
[As seen on the lefthand notebook page in the photo]
- When a game is a draw, players may together add a new row and new column, rendering the board a 16 square-space. (As I write I am aware there is likely unique nomenclature for “board” or “paper” games, e.g. a word for “board” that is more inclusive.) As part of this rule, a win is still gained by achieving 3 contiguous squares–not four.
–> Jonathan immediately won. We tried again,
… and got into an immediate discussion about the place of human behavior and computer-logic. As we build a new version of a game, are we building it so that there are multiple possible outcomes even for a computer, or are we depending on the human flaw of making error in not choosing the best square as a foundation of our new evolution? This came to light as we realized we needed to attempt multiple iterations of this new rule, with someone starting in the middle each time to determine whether Player 1 would “always” win (if both players are playing at their logical best) in this new rule. If that were the case, we were ready to throw out this rule and start anew. We were pressed for time, and decided to experiment with a replacement rule.
[As seen in the lower center & right two grid figures on the righthand page of the notebook in photo above]
2. A player may replace the other player’s mark on the grid by drawing their own mark over the other’s and forfeit any other move on that turn.
–> The player who first replaced one mark with another immediately won. So we threw out that rule.
3. (Must be played with pencils that have erasures) A player may erase another player’s mark, forfeiting their own turn. A player may replace an erased square (now newly “blank) with their own mark on their turn.
[As seen in the upper left and center grids on the righthand page of the notebook in photo above]
As we analyzed our own game and each other’s, we kept turning to the same question of the import of creating a game that would result in alternating wins by the most “rational” players, i.e. computers.
We shared with our colleagues. In examining S. & L.’s “Hangman” rules in which selected letters allow for a limb being erased, we discussed both implicit strategy–which may apply to the way rules contain many mini-rules, e.g. they allowed for more letters to be available in longer words. And, no doubt, that out of further rules, complexity may emerge. Jonathan and I discovered that rules can also pull in the opposite direction: some rules can engender a situation in which players automatically will win–if acting rationally–according to the order of turns.